Otro estupendo jueguecito para liarnos...
Enlace al juego
jueves, 31 de marzo de 2011
martes, 29 de marzo de 2011
lunes, 28 de marzo de 2011
Sumando...
Hace tiempo que no os propongo un reto...
Este me gustó, lo traigo del blog de Números y algo más... ( lo recomiendo )
-¿Corriste la maratón?
- Si fue fabuloso, corrimos entre 1000 y 2000 personas.
- ¿Hubo premios?
-Si, a cada corredor le dieron una camiseta con la posición en la que salió en la carrera.
-¿Y tu camiseta que número tiene?
- Es muy curioso, si sumamos los números de las camisetas de los que salieron delante mio, obtenemos el mismo resultado que si sumamos los números de las camisetas de los que salieron detrás mío.
¿En que posición salió el corredor?
Este me gustó, lo traigo del blog de Números y algo más... ( lo recomiendo )
-¿Corriste la maratón?
- Si fue fabuloso, corrimos entre 1000 y 2000 personas.
- ¿Hubo premios?
-Si, a cada corredor le dieron una camiseta con la posición en la que salió en la carrera.
-¿Y tu camiseta que número tiene?
- Es muy curioso, si sumamos los números de las camisetas de los que salieron delante mio, obtenemos el mismo resultado que si sumamos los números de las camisetas de los que salieron detrás mío.
¿En que posición salió el corredor?
domingo, 27 de marzo de 2011
martes, 22 de marzo de 2011
Descubriendo letras en matemáticas
Esta entrada es especialmente para los epsilones de 1º y 2º de la eso, los peques del insti.¿Tienes problemas con el álgebra?
¿Qué tal si repasamos algo...?
Abrir la aplicación en pantalla completa
¿Qué tal si repasamos algo...?
Abrir la aplicación en pantalla completa
lunes, 21 de marzo de 2011
Día de la poesía
Hoy se celebra en todo el mundo el día de la poesía.
Ya sabéis que a mi me gusta mucho..., y no quería dejar pasar este día sin celebrarlo con vosotros.
Para esta ocasión, dejo un podcast de un recital que ofreció Mario Benedetti en Mayo de 1996 en el Colegio Mayor Virgen de África de Madrid.
Buscad un momento tranquilo...
01 - Introducción.
02 - Sueldo.
03 - El nuevo.
04 - Después.
05 - Los pitucos.
06 - Corazón coraza.
07 - A La Izquierda Del Roble.
08 - Grietas.
09 - Quemar las naves.
10 - Oda a la pacificación.
11 - Táctica y estrategia.
12 - Viceversa.
13 - Los formales y el frío.
14 - Hagamos un trato.
15 - No te salves.
16 - Otro cielo.
17 - Botella al mar.
18 - Cálculo de probabilidades.
19 - Nuevo Canal Interoceánico.
20 - Contraofensiva.
21 - Síndrome.
22 - Ahora todo esta claro.
23 - Desaparecidos.
24 - Una mujer desnuda y en lo oscuro.
25 - Soneto (no tan) arbitrario.
26 - Terapia.
27 - Desde el alma (vals).
28 - Ese gran simulacro.
29 - Desganas.
30 - El pusilánime.
31 - La misma pócima.
32 - Pájaros.
33 - Mar de la memoria.
34 - Buenos días Gabriel.
35 - Retrato de verdugo con loro.
36 - El amor es un centro.
37 - Pies hermosos.
38 - La Octava.
39 - Señales.
40 - Despabilate amor.
41 - Trueque.
42 - Tíbulo.
Fuente: Audio de Juan López Ayala en ivoox
Aquí podéis encontrar algunas letras
Ya sabéis que a mi me gusta mucho..., y no quería dejar pasar este día sin celebrarlo con vosotros.
Para esta ocasión, dejo un podcast de un recital que ofreció Mario Benedetti en Mayo de 1996 en el Colegio Mayor Virgen de África de Madrid.
Buscad un momento tranquilo...
01 - Introducción.
02 - Sueldo.
03 - El nuevo.
04 - Después.
05 - Los pitucos.
06 - Corazón coraza.
07 - A La Izquierda Del Roble.
08 - Grietas.
09 - Quemar las naves.
10 - Oda a la pacificación.
11 - Táctica y estrategia.
12 - Viceversa.
13 - Los formales y el frío.
14 - Hagamos un trato.
15 - No te salves.
16 - Otro cielo.
17 - Botella al mar.
18 - Cálculo de probabilidades.
19 - Nuevo Canal Interoceánico.
20 - Contraofensiva.
21 - Síndrome.
22 - Ahora todo esta claro.
23 - Desaparecidos.
24 - Una mujer desnuda y en lo oscuro.
25 - Soneto (no tan) arbitrario.
26 - Terapia.
27 - Desde el alma (vals).
28 - Ese gran simulacro.
29 - Desganas.
30 - El pusilánime.
31 - La misma pócima.
32 - Pájaros.
33 - Mar de la memoria.
34 - Buenos días Gabriel.
35 - Retrato de verdugo con loro.
36 - El amor es un centro.
37 - Pies hermosos.
38 - La Octava.
39 - Señales.
40 - Despabilate amor.
41 - Trueque.
42 - Tíbulo.
Fuente: Audio de Juan López Ayala en ivoox
Aquí podéis encontrar algunas letras
viernes, 18 de marzo de 2011
jueves, 17 de marzo de 2011
Premio Internacional Educared 2011
Os animo a todos a participar en estos premios. Hay muchas modalidades.
Folleto informativo
Más información
Folleto informativo
Más información
miércoles, 16 de marzo de 2011
Museos del mundo
¿Conoces estos museos...?
Ahora puedes echar un vistazo sin salir de casa. Haz una visita en ART PROJECT
Y si te interesan las obras de un autor en particular, te invito a visitar esta web, seguro que encuentras lo que buscas...
Ahora puedes echar un vistazo sin salir de casa. Haz una visita en ART PROJECT
Y si te interesan las obras de un autor en particular, te invito a visitar esta web, seguro que encuentras lo que buscas...
lunes, 14 de marzo de 2011
La cuadratura del círculo
Hoy es un día señalado en mi agenda. Desde hace tiempo, hoy se celebra el día de Pi. La idea surgió de un estadounidense Larry Shaw ,ya que las fechas allí se escriben al revés que aquí, poniendo primero el mes y después el día, así, hoy es 3/14.
Para celebrarlo voy a contaros algo sobre este famoso número y uno de los problemas con más historia dentro del mundo de las matemáticas: la cuadratura del círculo.
Hace muchos, muchos años, el hombre quiso construir un cuadrado, pero no uno cualquiera, no.
Uno que tuviera el mismo área que el área de un círculo dado. (Es decir, yo te doy un círculo y tu me dibujas un cuadrado que tenga exactamente el mismo área del círculo.)
¿Por qué?...pues quizá porque es mucho más fácil calcular el área de un cuadrado... ¿verdad?
La construcción debía ser fácil...solo con la utilización de una regla y un compás; y, por supuesto, posible...es decir en un número finito de pasos.
Bueno, pues aquí tenéis enunciado el famoso problema de la cuadratura del círculo que trajo de cabeza a muchísimos matemáticos durante muchos, muchos años...hasta que en 1882 el alemán Lindemann echó un jarro de agua fría sobre el mismo...pero no adelantemos acontecimientos.
¿Alguien quiere intentarlo?
Bien, detengámonos un momento a pensar en la dificultad de llevar esto a cabo. Nosotros, ahora, sabemos que
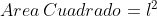
De manera que tendrá que ser
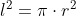
Y así
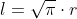
Si tomamos un radio unidad, nuestro problema se reduce a dibujar
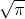
De hecho, si pudiéramos dibujar Pi, la raíz de Pi sería fácilmente construible
Por tanto nuestro problema se reduce a construir Pi con regla y compás...
Empecemos por el principio ¿Qué es Pi?
Pi es una constante que aparece en la relación de proporcionalidad que hay entre la longitud de una circunferencia cualquiera y su diámetro. No importa lo grande, o pequeña que sea nuestra circunferencia, pues su diámetro será también grande, o pequeño.
Un resultado que ahora damos por evidente es que esta constante, Pi, es la misma que aparece en el área del círculo, pero fue Arquímedes quien demostró este resultado.
Arquímedes demostró que el área que determina una circunferencia de radio r, es la misma que el área de un triángulo rectángulo de base la longitud de la circunferencia y de altura el radio r.
Ahora bien, me preguntaréis...¿cómo demostró esto Arquímedes, si no podía construir ese triángulo con regla y compás?
La demostración que utilizó se denomina en matemáticas, demostración por reducción al absurdo.
¿Qué?...Absurdo??...Pues sí...
Si suponemos que algo es cierto y después de seguir un razonamiento lógico, llegamos a una contradicción, es decir a un absurdo, como por ejemplo a que 2 = 0, entonces el punto de partida es falso.
Esta es la demostración de Arquímedes:
Arquímedes utilizó estos polígonos inscritos y circunscritos a la circunferencia para aproximar Pi.
No solo llegó a una estupenda aproximación de Pi, es más, ideó un algoritmo que fué utilizado por muchos matemáticos después. La idea es calcular Pi con tanta precisión como queramos, utilizando las áreas de polígonos inscritos y circunscritos, doblando sus lados en cada iteración. La pena es que esta serie converge muy, muy lentamente.
Utilizando las fórmulas recurrentes:
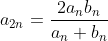
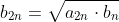
Siendo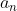
el perímetro del polígono de n lados circunscrito y 
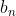el perímetro del polígono de n lados inscrito.
Aquí tienes una demostración.
Sin embargo no fue este el algoritmo que Arquímedes utilizó. Los cálculos de Arquímedes se basan en la semejanza de triángulos, el teorema de Pitágoras y muy en particular en la proposición 3 del libro VI de los elementos de Euclides.
Esta proposición dice que al trazar una bisectriz en un ángulo de un triángulo, esta determina un punto en el lado opuesto que divide a este lado en partes proporcionales a los otros dos lados del triángulo.
Os dejo un par de animaciones en flash:
Tener en cuenta que Arquímedes no tenía calculadora, y consiguió unas estupendas aproximaciones a las raíces que aparecen en los cálculos.
Pues después de muchos cálculos y muchos matemáticos que intentaron acercarse a Pi, resulta que este número es trascendente, es decir no es un número algebraico, no es solución de ninguna ecuación polinómoca con coeficientes racionales, y por tanto no es un número construible con regla y compás.
Con esta entrada participo en la Edición 2.2 del Carnaval de Matemáticas cuyo anfitrión, en este mes, es Gaussianos.
Para celebrarlo voy a contaros algo sobre este famoso número y uno de los problemas con más historia dentro del mundo de las matemáticas: la cuadratura del círculo.
Hace muchos, muchos años, el hombre quiso construir un cuadrado, pero no uno cualquiera, no.
Uno que tuviera el mismo área que el área de un círculo dado. (Es decir, yo te doy un círculo y tu me dibujas un cuadrado que tenga exactamente el mismo área del círculo.)
¿Por qué?...pues quizá porque es mucho más fácil calcular el área de un cuadrado... ¿verdad?
La construcción debía ser fácil...solo con la utilización de una regla y un compás; y, por supuesto, posible...es decir en un número finito de pasos.
Bueno, pues aquí tenéis enunciado el famoso problema de la cuadratura del círculo que trajo de cabeza a muchísimos matemáticos durante muchos, muchos años...hasta que en 1882 el alemán Lindemann echó un jarro de agua fría sobre el mismo...pero no adelantemos acontecimientos.
¿Alguien quiere intentarlo?
Bien, detengámonos un momento a pensar en la dificultad de llevar esto a cabo. Nosotros, ahora, sabemos que
De manera que tendrá que ser
Y así
Si tomamos un radio unidad, nuestro problema se reduce a dibujar
De hecho, si pudiéramos dibujar Pi, la raíz de Pi sería fácilmente construible
Empecemos por el principio ¿Qué es Pi?
Pi es una constante que aparece en la relación de proporcionalidad que hay entre la longitud de una circunferencia cualquiera y su diámetro. No importa lo grande, o pequeña que sea nuestra circunferencia, pues su diámetro será también grande, o pequeño.
Un resultado que ahora damos por evidente es que esta constante, Pi, es la misma que aparece en el área del círculo, pero fue Arquímedes quien demostró este resultado.
Arquímedes demostró que el área que determina una circunferencia de radio r, es la misma que el área de un triángulo rectángulo de base la longitud de la circunferencia y de altura el radio r.
Ahora bien, me preguntaréis...¿cómo demostró esto Arquímedes, si no podía construir ese triángulo con regla y compás?
La demostración que utilizó se denomina en matemáticas, demostración por reducción al absurdo.
¿Qué?...Absurdo??...Pues sí...
Si suponemos que algo es cierto y después de seguir un razonamiento lógico, llegamos a una contradicción, es decir a un absurdo, como por ejemplo a que 2 = 0, entonces el punto de partida es falso.
Esta es la demostración de Arquímedes:
Arquímedes utilizó estos polígonos inscritos y circunscritos a la circunferencia para aproximar Pi.
No solo llegó a una estupenda aproximación de Pi, es más, ideó un algoritmo que fué utilizado por muchos matemáticos después. La idea es calcular Pi con tanta precisión como queramos, utilizando las áreas de polígonos inscritos y circunscritos, doblando sus lados en cada iteración. La pena es que esta serie converge muy, muy lentamente.
Utilizando las fórmulas recurrentes:
Siendo
Aquí tienes una demostración.
Sin embargo no fue este el algoritmo que Arquímedes utilizó. Los cálculos de Arquímedes se basan en la semejanza de triángulos, el teorema de Pitágoras y muy en particular en la proposición 3 del libro VI de los elementos de Euclides.
Esta proposición dice que al trazar una bisectriz en un ángulo de un triángulo, esta determina un punto en el lado opuesto que divide a este lado en partes proporcionales a los otros dos lados del triángulo.
Os dejo un par de animaciones en flash:
Tener en cuenta que Arquímedes no tenía calculadora, y consiguió unas estupendas aproximaciones a las raíces que aparecen en los cálculos.
Pues después de muchos cálculos y muchos matemáticos que intentaron acercarse a Pi, resulta que este número es trascendente, es decir no es un número algebraico, no es solución de ninguna ecuación polinómoca con coeficientes racionales, y por tanto no es un número construible con regla y compás.
Con esta entrada participo en la Edición 2.2 del Carnaval de Matemáticas cuyo anfitrión, en este mes, es Gaussianos.
martes, 8 de marzo de 2011
jueves, 3 de marzo de 2011
miércoles, 2 de marzo de 2011
Suscribirse a:
Entradas (Atom)
Entradas
