Ahora que ya está acabado el curso, y empiezan las vacaciones, es tiempo de juegos...desde el blog de Jugando en clase os traigo este reto lógico de 100 niveles. Si pasáis del 15, por favor escribidme un comentario...
jueves, 30 de junio de 2011
miércoles, 29 de junio de 2011
Anillos. ( Segunda parte )
Antes de poder articular un alegre “buenos días”…
-Hemos solucionado el problema para poder formar grupo con las aplicaciones de un conjunto
-¿De veras? Contadme.
- Basta considerar únicamente aplicaciones biyectivas, es decir que cada elemento se corresponda con un único elemento y viceversa, todo elemento tenga una única imagen. De esta manera no tenemos problemas al tomar la aplicación inversa.
-Muy bien chicos. Problema solucionado.
Hemos construido un grupo ( G,◦ ) , con G = Aut(X) = {Aplicaciones biyectivas de X en X} y la aplicación: GxG → G , (g,g’) → g ◦ g’ la composición de aplicaciones, que verifica las tres propiedades: asociativa, existe elemento neutro que es la aplicación identidad y para todo elemento g existe su inverso g-1 ,que es la aplicación inversa que existe por ser g biyectiva.
Este es un buen ejemplo de grupo no conmutativo, puesto que la composición de aplicaciones no verifica la propiedad conmutativa. En general no es lo mismo g ◦ g’ que g’◦ g.
Este grupo que acabáis de construir es muy importante en matemáticas, y en particular cuando el conjunto a considerar son los primeros n números naturales, X = {1,2,3,…,n}, entonces se denomina de una manera especial: grupo simétrico n-ésimo.
-Entonces los elementos del grupo serían permutaciones.
-Efectivamente... ¿cuántos elementos tendría este grupo?
-n! = n·(n-1)·(n-2)···2·1
-Muy bien, veo que hoy estáis más receptivos…
Dentro de un grupo, podemos considerar subgrupos, que serían subconjuntos del grupo, pero manteniendo la estructura, es decir tendrían el elemento neutro, y para cada elemento su inverso, además dados dos elementos del subconjunto su producto también estaría dentro del subconjunto, por ejemplo dentro del grupo simétrico tenemos los grupos diedrales, que se corresponden con las simetrías de un polígono regular de n lados (rotaciones y reflexiones especulares).
Si quieres profundizar lee este artículo, visita esta página y experimenta con Kali
Y hablando de geometría, hay un grupo llamado afín unidimensional, que tampoco es conmutativo, el conjunto está formado por pares de números reales, el primero distinto de cero.
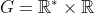
La aplicación que le da esa estructura de grupo es la siguiente:
\times (\mathbb{R}^{*}\times \mathbb{R})&\rightarrow & (\mathbb{R}^{*}\times \mathbb{R}) & \\ (\left ( \lambda ,a \right ),\left ( \lambda ',a' \right ))& \rightarrow &\left ( \lambda ,a \right )*\left ( \lambda ',a' \right )\left = ( \lambda \cdot \lambda ',\lambda \cdot a'+a \right ) & \end{matrix})
¿cuál sería el elemento neutro?
-El (1,0) porque ( λ , a ) * ( 1 , 0 ) = ( λ·1 , λ·0+a ) = ( λ , a )
-Muy bien!! Y ¿cuál sería el elemento inverso de ( λ , a )?
-Tendría que verificar ( λ , a ) * ( m , b ) = ( 1 , 0 ).
Podemos resolver la ecuación
λ · m = 1, luego m =1/λ, y
λ · b + a = 0, luego b = -a/λ.
Es decir
^{-1}=(\frac{1}{\lambda },-\frac{a}{\lambda }))
Claro! Por eso λ no puede ser cero!
-Perfecto chicos. Este grupo es importante porque establece los invariantes geométricos al actuar sobre un conjunto de “puntos”. Sin entrar en detalles, digamos que el primer número se utiliza para dilatar (se multiplica) y el segundo número se utiliza para trasladar (se suma).
-Otro ejemplo de grupo no conmutativo es el grupo general lineal cuyo conjunto es el de matrices cuadradas de orden n de números reales. ¿Recordáis las matrices?
-Sí, las “cajas” de números, pero solo operamos con las de orden dos y tres.
-Bueno, se puede generalizar hasta el orden que queráis, pero si os resulta más fácil, considerar las de orden dos. Tomemos como aplicación para nuestro grupo, la multiplicación de matrices, que es asociativa. ¿Cuál sería el elemento neutro?
-La matriz identidad, esa que tiene unos en la diagonal y el resto ceros.
-Bien, y… ¿hay elemento inverso?
-Solo tenían inversa las matrices con determinante distinto de cero.
-Pues entonces… ¿cúal sería nuestro conjunto?
-Las matrices cuadradas con determinante distinto de cero.
-Estupendo, veo que vais entendiendo la estructura del grupo… Dentro hay varios subgrupos importantes. Sería un estupendo trabajo buscar algún subgrupo, por ejemplo ¿qué pasa si tomamos matrices cuyo determinante sea la unidad, formarían subgrupo?, ¿y si tomamos matrices, que verifiquen que ellas por sus traspuestas sean la matriz identidad?
-Un último ejemplo de grupo, esta vez conmutativo, y uno de mis preferidos, es el grupo formado por el conjunto de las clases de restos módulo n.
-Eso si que no nos suena de nada…
Veamos…
Consideremos el conjunto de los números enteros. Y elijamos un n particular, venga, un número cualquiera…
-El cinco
-Vale, aunque ya sabéis que podemos fijar cualquiera, en este caso n será cinco. Vamos a formar un conjunto de solo cinco elementos, pero vamos a tener en cuenta a todos los números enteros. ¿Cómo lo hacemos?
-A ver si lo he entendido..., ¿cogemos todos los enteros y los agrupamos en cinco clases?
-Eso es…¿alguna idea?
-Puedo cambiar n?
-Bueno
-Pues n=2
-Y ¿por qué cambias a dos?
-Porque podemos hacer dos clases: pares e impares.
-Estupendo, no esta mal para empezar. ¿Dónde colocamos el cero?
-Pues no sé… venga pues n=3, pares, impares y el cero.
-Eso me gusta menos… ¿Os acordáis de la expresión algebraica que usábamos para los pares y los impares?
-Si, si…2x y 2x+1, donde x podía ser cualquier número.
-Bien, pues ¿que encaja mejor con el cero?
- 2·0=0, con los pares?
- Bueno, es la mejor opción. Realmente lo que hacemos para saber si un número es par es dividirlo entre dos y si la división es exacta resulta que es par, en caso contrario sería impar. Nuestro caso para n=2 está resuelto, pero ¿y si n = 3? ¿qué hacemos?
…Silencio…
-Veamos, si dividimos cualquier número entre 3, ¿qué restos podemos obtener?
-0 , si la división es exacta, 1 y 2
-Y si dividimos por 5
-0, 1, 2, 3 y 4
- Ya lo tenéis, esas serán las clases de restos módulo 5. Y tenemos en cuenta a todos los números! Ahora necesitamos una operación para el grupo ¿cuál?
-La suma
-Vale, pero podemos definir una suma +n "especial" : a +n b = resto de dividir a+b por n.
donde n en nuestro caso particular es cinco. Perfecto, la suma es asociativa. ¿cuál sería el elemento neutro?
-el cero
-¿Qué números entrarían dentro de esta clase?, es decir ¿qué números al dividir por cinco tienen de resto cero?
-5, 10, 15, 20…todos los múltiplos de cinco
-Perfecto, todos esos números estarían en la clase del elemento neutro. Muy bien. Y ¿cuál sería el inverso del 1?
-El -1?
-Estamos en un conjunto donde solo hay cinco elementos {0,1,2,3,4}, y hemos clasificado a todos los números, es decir el -1 estaría en una de estas clases ¿en cuál?
- Pero -1 es menor que cinco y no podemos dividirlo…
-Vale, pero al -1 podéis sumarle cualquier múltiplo de cinco, porque sería como sumarle cero...
-Entonces -1 estaría en la misma clase que el 4
-No solo eso, sino que el 4 sería el inverso del 1, porque 1+4=5=0
-Ahh…ya lo he entendido!! Entonces el inverso del 2 sería el 3, y el inverso del 3 el 2, y el inverso del 4 el 1…
-Eso es, todo elemento tiene su inverso…¡Tenemos grupo!
Creo que ya estáis preparados para conocer a su hermano mayor: el Anillo
Pero eso será otro día pequeñuelos…
Esta entrada también participa en la edición 2.5 del Carnaval de Matemáticas donde ya podéis visitar algunos estupendos post del carnaval, y a nuestro anfitrión que está haciendo un estupendo trabajo: Juegos Topológicos
-Hemos solucionado el problema para poder formar grupo con las aplicaciones de un conjunto
-¿De veras? Contadme.
- Basta considerar únicamente aplicaciones biyectivas, es decir que cada elemento se corresponda con un único elemento y viceversa, todo elemento tenga una única imagen. De esta manera no tenemos problemas al tomar la aplicación inversa.
-Muy bien chicos. Problema solucionado.
Hemos construido un grupo ( G,◦ ) , con G = Aut(X) = {Aplicaciones biyectivas de X en X} y la aplicación: GxG → G , (g,g’) → g ◦ g’ la composición de aplicaciones, que verifica las tres propiedades: asociativa, existe elemento neutro que es la aplicación identidad y para todo elemento g existe su inverso g-1 ,que es la aplicación inversa que existe por ser g biyectiva.
Este es un buen ejemplo de grupo no conmutativo, puesto que la composición de aplicaciones no verifica la propiedad conmutativa. En general no es lo mismo g ◦ g’ que g’◦ g.
Este grupo que acabáis de construir es muy importante en matemáticas, y en particular cuando el conjunto a considerar son los primeros n números naturales, X = {1,2,3,…,n}, entonces se denomina de una manera especial: grupo simétrico n-ésimo.
-Entonces los elementos del grupo serían permutaciones.
-Efectivamente... ¿cuántos elementos tendría este grupo?
-n! = n·(n-1)·(n-2)···2·1
-Muy bien, veo que hoy estáis más receptivos…
Dentro de un grupo, podemos considerar subgrupos, que serían subconjuntos del grupo, pero manteniendo la estructura, es decir tendrían el elemento neutro, y para cada elemento su inverso, además dados dos elementos del subconjunto su producto también estaría dentro del subconjunto, por ejemplo dentro del grupo simétrico tenemos los grupos diedrales, que se corresponden con las simetrías de un polígono regular de n lados (rotaciones y reflexiones especulares).
Si quieres profundizar lee este artículo, visita esta página y experimenta con Kali
Y hablando de geometría, hay un grupo llamado afín unidimensional, que tampoco es conmutativo, el conjunto está formado por pares de números reales, el primero distinto de cero.
La aplicación que le da esa estructura de grupo es la siguiente:
¿cuál sería el elemento neutro?
-El (1,0) porque ( λ , a ) * ( 1 , 0 ) = ( λ·1 , λ·0+a ) = ( λ , a )
-Muy bien!! Y ¿cuál sería el elemento inverso de ( λ , a )?
-Tendría que verificar ( λ , a ) * ( m , b ) = ( 1 , 0 ).
Podemos resolver la ecuación
λ · m = 1, luego m =1/λ, y
λ · b + a = 0, luego b = -a/λ.
Es decir
Claro! Por eso λ no puede ser cero!
-Perfecto chicos. Este grupo es importante porque establece los invariantes geométricos al actuar sobre un conjunto de “puntos”. Sin entrar en detalles, digamos que el primer número se utiliza para dilatar (se multiplica) y el segundo número se utiliza para trasladar (se suma).
-Otro ejemplo de grupo no conmutativo es el grupo general lineal cuyo conjunto es el de matrices cuadradas de orden n de números reales. ¿Recordáis las matrices?
-Sí, las “cajas” de números, pero solo operamos con las de orden dos y tres.
-Bueno, se puede generalizar hasta el orden que queráis, pero si os resulta más fácil, considerar las de orden dos. Tomemos como aplicación para nuestro grupo, la multiplicación de matrices, que es asociativa. ¿Cuál sería el elemento neutro?
-La matriz identidad, esa que tiene unos en la diagonal y el resto ceros.
-Bien, y… ¿hay elemento inverso?
-Solo tenían inversa las matrices con determinante distinto de cero.
-Pues entonces… ¿cúal sería nuestro conjunto?
-Las matrices cuadradas con determinante distinto de cero.
-Estupendo, veo que vais entendiendo la estructura del grupo… Dentro hay varios subgrupos importantes. Sería un estupendo trabajo buscar algún subgrupo, por ejemplo ¿qué pasa si tomamos matrices cuyo determinante sea la unidad, formarían subgrupo?, ¿y si tomamos matrices, que verifiquen que ellas por sus traspuestas sean la matriz identidad?
-Un último ejemplo de grupo, esta vez conmutativo, y uno de mis preferidos, es el grupo formado por el conjunto de las clases de restos módulo n.
-Eso si que no nos suena de nada…
Veamos…
Consideremos el conjunto de los números enteros. Y elijamos un n particular, venga, un número cualquiera…
-El cinco
-Vale, aunque ya sabéis que podemos fijar cualquiera, en este caso n será cinco. Vamos a formar un conjunto de solo cinco elementos, pero vamos a tener en cuenta a todos los números enteros. ¿Cómo lo hacemos?
-A ver si lo he entendido..., ¿cogemos todos los enteros y los agrupamos en cinco clases?
-Eso es…¿alguna idea?
-Puedo cambiar n?
-Bueno
-Pues n=2
-Y ¿por qué cambias a dos?
-Porque podemos hacer dos clases: pares e impares.
-Estupendo, no esta mal para empezar. ¿Dónde colocamos el cero?
-Pues no sé… venga pues n=3, pares, impares y el cero.
-Eso me gusta menos… ¿Os acordáis de la expresión algebraica que usábamos para los pares y los impares?
-Si, si…2x y 2x+1, donde x podía ser cualquier número.
-Bien, pues ¿que encaja mejor con el cero?
- 2·0=0, con los pares?
- Bueno, es la mejor opción. Realmente lo que hacemos para saber si un número es par es dividirlo entre dos y si la división es exacta resulta que es par, en caso contrario sería impar. Nuestro caso para n=2 está resuelto, pero ¿y si n = 3? ¿qué hacemos?
…Silencio…
-Veamos, si dividimos cualquier número entre 3, ¿qué restos podemos obtener?
-0 , si la división es exacta, 1 y 2
-Y si dividimos por 5
-0, 1, 2, 3 y 4
- Ya lo tenéis, esas serán las clases de restos módulo 5. Y tenemos en cuenta a todos los números! Ahora necesitamos una operación para el grupo ¿cuál?
-La suma
-Vale, pero podemos definir una suma +n "especial" : a +n b = resto de dividir a+b por n.
donde n en nuestro caso particular es cinco. Perfecto, la suma es asociativa. ¿cuál sería el elemento neutro?
-el cero
-¿Qué números entrarían dentro de esta clase?, es decir ¿qué números al dividir por cinco tienen de resto cero?
-5, 10, 15, 20…todos los múltiplos de cinco
-Perfecto, todos esos números estarían en la clase del elemento neutro. Muy bien. Y ¿cuál sería el inverso del 1?
-El -1?
-Estamos en un conjunto donde solo hay cinco elementos {0,1,2,3,4}, y hemos clasificado a todos los números, es decir el -1 estaría en una de estas clases ¿en cuál?
- Pero -1 es menor que cinco y no podemos dividirlo…
-Vale, pero al -1 podéis sumarle cualquier múltiplo de cinco, porque sería como sumarle cero...
-Entonces -1 estaría en la misma clase que el 4
-No solo eso, sino que el 4 sería el inverso del 1, porque 1+4=5=0
-Ahh…ya lo he entendido!! Entonces el inverso del 2 sería el 3, y el inverso del 3 el 2, y el inverso del 4 el 1…
-Eso es, todo elemento tiene su inverso…¡Tenemos grupo!
Creo que ya estáis preparados para conocer a su hermano mayor: el Anillo
Pero eso será otro día pequeñuelos…
Esta entrada también participa en la edición 2.5 del Carnaval de Matemáticas donde ya podéis visitar algunos estupendos post del carnaval, y a nuestro anfitrión que está haciendo un estupendo trabajo: Juegos Topológicos
Etiquetas:
carnaval de matemáticas,
matemáticas,
Retos
martes, 28 de junio de 2011
Anillos. ( Primera parte )
¿Qué es un anillo?, si asaltas con esta pregunta en clase, todos los alumnos coinciden más o menos en sus respuestas:
Una sortija para colocar en el dedo..., un aro que representa el compromiso en algunas religiones, como el sacramento del matrimonio... una formación celeste que circunda determinados planetas… Incluso alguno le echa imaginación; La sección de un cilindro cortado por dos planos paralelos entre sí y perpendiculares al eje del cilindro.
Pues no. No van por ahí los tiros.
Un anillo en matemáticas es el nombre de una estructura...
Pero antes tenemos que hablar de su hermano pequeño: el grupo.
-¿Qué diríais vosotros que es un grupo?
-Un conjunto de cosas o de personas...
-Entonces... ¿Qué diferencia hay entre un grupo y un conjunto?
...breve silencio…
-Quizá se utiliza grupo, cuando es un conjunto de personas o cosas con alguna relación entre ellas.
Bueno vamos bien…
En matemáticas un grupo se forma dentro de un conjunto donde definimos una aplicación en la que a cada par de elementos del conjunto le hacemos corresponder otro elemento del conjunto. Esto lo denotamos:
Y además esta aplicación verifica tres cosas:
1. Es asociativa.
2. Posee elemento neutro.
3. Cada elemento del grupo tiene su inverso.
Fijaos que el elemento neutro es único.
Una pista: supongamos que hay dos diferentes…e y e’.
Por un lado e+e’=e por ser e’ elemento neutro, pero por otro lado e+e’=e’ por ser e elemento neutro, luego e=e’.
Bueno…
- ¿Habéis entendido algo?
Todos copiando como locos, y nadie responde.
Veamos...
-¿Qué es una aplicación?
...Silencio sepulcral...
-¿Y una función?
Esto a todos les suena más.
-Es cuando a un número le hacemos corresponder otro: y = f(x).
-Bueno, no es del todo exacto. ¿Alguno puede hacer una representación gráfica de una función?
Sale un valiente a la pizarra y dibuja unos ejes de coordenadas y una recta, nos explica que el eje horizontal representa los números reales, el conjunto de partida, y el eje vertical también son los números reales, el conjunto de llegada, y que para cada número real x hay un número real y=f(x).
-Perfecto, pero si dibujo una circunferencia…¿qué es lo que falla?
Todos se dan cuenta de que si tomo un número en el eje horizontal, tengo dos imágenes ¿cuál tomamos?
-Eso no es una función.
-No, no lo es. Entonces ¿qué es una función?
-A cada punto del conjunto inicial le hacemos corresponder un único punto del conjunto final.
-Muy bien chicos. Se llama función cuando los conjuntos son numéricos, por ejemplo la recta que está pintada en la pizarra es una función real de variable real. Si el conjunto no es numérico se suele utilizar la palabra aplicación. Por ejemplo:
Sí es aplicación
Sí es aplicación
NO es aplicación
NO es aplicación
-Consideremos un conjunto y veamos si podríamos formar un grupo con él. ¿Alguna sugerencia?
-Los números naturales.
-¿Y la aplicación?
-La suma.
-¡Qué poca imaginación!...pero veamos… ¿Forman grupo?
Es asociativa…, tiene elemento neutro ( suponiendo que el cero está contenido en los números naturales), ¿Todo elemento tiene inverso?...pues no. No nos sirve.
-Entonces con los números enteros.
-¡Muy bien! Los números enteros con la suma, verifican las tres propiedades.
Además este grupo verifica la propiedad conmutativa, pues para todo par de números enteros a y b se verifica a+b=b+a. A estos grupos se les llama grupos conmutativos o abelianos, pero hay otros grupos que no son conmutativos. Busquemos un ejemplo. ¿Alguna idea?
-No podemos coger como conjuntos los números racionales, ni los reales, porque todos verifican la propiedad conmutativa...
- Pues pensad en conjuntos de otras cosas, que no sean números.
…Silencio sepulcral…
-Hemos hablado de aplicaciones… y si tomamos, por ejemplo, aplicaciones en vez de números?
-¿Aplicaciones?... pero ¿eso sirve?
-Bueno..., intentémoslo a ver que sale. Imaginemos un conjunto de cosas, las que queráis y consideremos todas las posibles aplicaciones entre ese conjunto y él mismo:
-¿Qué operación podemos hacer con las aplicaciones?
-Sumarlas
-Tened en cuenta que no estamos trabajando con conjuntos numéricos, por tanto no tiene sentido la suma.
-Ya lo tengo!...la composición de funciones!
-Fenomenal!, pero no hablamos de funciones ¿te acuerdas?...Dadas dos aplicaciones, llamémoslas g y g’, la composición es otra aplicación, es hacer una y seguida la otra... así que...nos sirve.
-Veamos si verifican las tres propiedades:
Es asociativa, la demostración os la dejo a vosotros…
Tiene elemento neutro: la aplicación identidad que asocia a cada elemento el mismo.
¿Existe la aplicación inversa? Sería hacer el recorrido empezando por el final...aquí tenemos un problemilla…¿alguien me dice cuál es?
-En el ejemplo anterior si hacemos el camino al contrario, la manzana tendría dos imágenes y las cerezas no tendrían imagen, no sería aplicación!!
-Bien, entonces...¿cómo lo arreglamos?
Os dejo pensarlo tranquilamente y continuamos mañana…
Con esta entrada participo en la edición 2.5 del Carnaval de Matemáticas que tiene por anfitrión un estupendo blog: Juegos Topológicos
Etiquetas:
carnaval de matemáticas,
matemáticas,
Retos
lunes, 20 de junio de 2011
Fibi está triste
Hola pequeños epsilones, hace tiempo que no os propongo un reto...Aquí os traigo uno:
 Mi nombre es Fibi, soy una alegre letra equis, pero últimamente estoy algo decaída, hace tiempo que desapareció mi querido número cinco, con el que llegué a formar monomio y a mantener una estrecha amistad.
Mi nombre es Fibi, soy una alegre letra equis, pero últimamente estoy algo decaída, hace tiempo que desapareció mi querido número cinco, con el que llegué a formar monomio y a mantener una estrecha amistad.
Añoro los tiempos en los que era la gran incógnita de una estupenda ecuación de segundo grado.Compartía parcela con dos vecinos extraordinarios, otra letra equis que había conseguido subir de grado y nunca se quitaba su elegante sombrero por donde asomaba un pequeño número dos, y la señora Matilde, que aunque era un número muy independiente también era especialmente amable, se llevaba bien con todo el mundo y tenía grandes amistades con pares y con impares.
 El muro estaba siempre vigilado por el señor Vicente, un estirado y serio símbolo igual, que nunca abandonaba su sitio. Al otro lado del muro estaba un silencioso y tímido número, el cero, del que nuca supe su nombre. Era tan especial que siempre estaba solo y cuando alguno de nosotros pasaba el muro, él desaparecía.
El muro estaba siempre vigilado por el señor Vicente, un estirado y serio símbolo igual, que nunca abandonaba su sitio. Al otro lado del muro estaba un silencioso y tímido número, el cero, del que nuca supe su nombre. Era tan especial que siempre estaba solo y cuando alguno de nosotros pasaba el muro, él desaparecía.
Un día pasó algo extraordinario de lo que no tengo explicación, la verdad es que me quedé dormida y cuando desperté, todos se habían ido, incluso mi compañero, el número cinco que nunca se separaba de mí.
Miré por encima del muro y allí estaba, algo cambiado, pues siempre que pasamos el muro, el señor Vicente nos quita nuestro signo y nos devuelve el contrario. Es una rutina obligada al pasar al otro lado, y el señor Vicente, el símbolo igual, es muy riguroso con esta norma, y si no lo hacemos, no nos deja pasar.
Más alejada estaba la señora Matilde, aunque ella formaba parte de un grupo muy peculiar, al que yo no había visto antes, le acompañaba un hermoso número cuatro y delante de ellos un cuadrado perfecto. La señora Matilde y sus acompañantes estaban atrapados dentro de una raíz. ¡Pobres!...
Yo ya tuve la experiencia de pasar por una raíz. ¡Son insaciables! Hace ya tiempo, cuando conseguí subir de orden y adquirir el ansiado sombrero con el pequeño número dos, cosa nada fácil, pues no abundan las letras equis que quieran multiplicarse conmigo, entonces llegó una raíz y ¡zas! en un plis-plas me quitó el sombrerito y desapareció.
Ahora, cuando veo alguna, salgo corriendo, porque si encima no tienes sombrerito se quedan contigo para siempre... o hasta encontrar otra letra equis con una raíz a cuestas, que quiera multiplicarse contigo, y esto es todavía más difícil.

Pues bien, allí estaban todos, sentados encima de una línea y debajo, un espectacular número dos, grande y fuerte, que parecía que sostuviera él solo a todos los demás.
Yo, como me sentía tan sola y parecía que al otro lado lo estaban pasando en grande, ni corta ni perezosa, le cambié el signo al señor Vicente y pasé al otro lado. Al mirar atrás, comprobé que aparecía el misterioso número cero ocupando el otro lado del muro. Corrí a reunirme con mi compañero, me costó saltar hasta la línea y una vez arriba, mi querido número cinco no quería ni acercarse a mí.
-¿Qué haces? ¡Tienes que irte al otro lado!
-Me quedé dormida. Lo siento ¿No quieres que sigamos juntos?- le dije
-Ya no podemos. Mira quién está junto a ti.
Yo volví la vista y allí, a mi lado, había aparecido de repente un número dos.
-Hola –le dije-¡Qué sorpresa!
-Creo que andas despistada. No deberías estar aquí. Vuelve ahora mismo al otro lado del muro, este no es lugar para ti. ¿No te das cuenta de que han resuelto la ecuación?...Nos vamos todos y tú no puedes venir.
A mí me hubiera gustado seguir allí, pero estaba claro que no era bien recibida, así que salte de la línea, el número dos, que había aparecido pegado a mi, desapareció enseguida y volví al otro lado del muro dejando el signo menos al señor Vicente, que pareció no inmutarse.
Ni siquiera pude hablar una palabra con el número cero, que también desapareció... la verdad es que no hay manera de pillarlo.
Me asomé a ver lo que ocurría en el otro lado y enseguida todo se transformó, la línea, la raíz, mi querido cinco, el espectacular número dos…¡todo desapareció! y en su lugar aparecieron dos números. A uno de ellos pude verle bien, era un precioso tres.
¿Cuál es el otro número que aparece con el tres?¿Puedes ayudar a Fibi y escribir la ecuación de segundo grado donde aparezca con su querido número cinco? ¿Qué número es Matilde?
 Mi nombre es Fibi, soy una alegre letra equis, pero últimamente estoy algo decaída, hace tiempo que desapareció mi querido número cinco, con el que llegué a formar monomio y a mantener una estrecha amistad.
Mi nombre es Fibi, soy una alegre letra equis, pero últimamente estoy algo decaída, hace tiempo que desapareció mi querido número cinco, con el que llegué a formar monomio y a mantener una estrecha amistad. Añoro los tiempos en los que era la gran incógnita de una estupenda ecuación de segundo grado.Compartía parcela con dos vecinos extraordinarios, otra letra equis que había conseguido subir de grado y nunca se quitaba su elegante sombrero por donde asomaba un pequeño número dos, y la señora Matilde, que aunque era un número muy independiente también era especialmente amable, se llevaba bien con todo el mundo y tenía grandes amistades con pares y con impares.
 El muro estaba siempre vigilado por el señor Vicente, un estirado y serio símbolo igual, que nunca abandonaba su sitio. Al otro lado del muro estaba un silencioso y tímido número, el cero, del que nuca supe su nombre. Era tan especial que siempre estaba solo y cuando alguno de nosotros pasaba el muro, él desaparecía.
El muro estaba siempre vigilado por el señor Vicente, un estirado y serio símbolo igual, que nunca abandonaba su sitio. Al otro lado del muro estaba un silencioso y tímido número, el cero, del que nuca supe su nombre. Era tan especial que siempre estaba solo y cuando alguno de nosotros pasaba el muro, él desaparecía.Un día pasó algo extraordinario de lo que no tengo explicación, la verdad es que me quedé dormida y cuando desperté, todos se habían ido, incluso mi compañero, el número cinco que nunca se separaba de mí.
Miré por encima del muro y allí estaba, algo cambiado, pues siempre que pasamos el muro, el señor Vicente nos quita nuestro signo y nos devuelve el contrario. Es una rutina obligada al pasar al otro lado, y el señor Vicente, el símbolo igual, es muy riguroso con esta norma, y si no lo hacemos, no nos deja pasar.
Más alejada estaba la señora Matilde, aunque ella formaba parte de un grupo muy peculiar, al que yo no había visto antes, le acompañaba un hermoso número cuatro y delante de ellos un cuadrado perfecto. La señora Matilde y sus acompañantes estaban atrapados dentro de una raíz. ¡Pobres!...
Yo ya tuve la experiencia de pasar por una raíz. ¡Son insaciables! Hace ya tiempo, cuando conseguí subir de orden y adquirir el ansiado sombrero con el pequeño número dos, cosa nada fácil, pues no abundan las letras equis que quieran multiplicarse conmigo, entonces llegó una raíz y ¡zas! en un plis-plas me quitó el sombrerito y desapareció.
Ahora, cuando veo alguna, salgo corriendo, porque si encima no tienes sombrerito se quedan contigo para siempre... o hasta encontrar otra letra equis con una raíz a cuestas, que quiera multiplicarse contigo, y esto es todavía más difícil.

Pues bien, allí estaban todos, sentados encima de una línea y debajo, un espectacular número dos, grande y fuerte, que parecía que sostuviera él solo a todos los demás.
Yo, como me sentía tan sola y parecía que al otro lado lo estaban pasando en grande, ni corta ni perezosa, le cambié el signo al señor Vicente y pasé al otro lado. Al mirar atrás, comprobé que aparecía el misterioso número cero ocupando el otro lado del muro. Corrí a reunirme con mi compañero, me costó saltar hasta la línea y una vez arriba, mi querido número cinco no quería ni acercarse a mí.
-¿Qué haces? ¡Tienes que irte al otro lado!
-Me quedé dormida. Lo siento ¿No quieres que sigamos juntos?- le dije
-Ya no podemos. Mira quién está junto a ti.
Yo volví la vista y allí, a mi lado, había aparecido de repente un número dos.
-Hola –le dije-¡Qué sorpresa!
-Creo que andas despistada. No deberías estar aquí. Vuelve ahora mismo al otro lado del muro, este no es lugar para ti. ¿No te das cuenta de que han resuelto la ecuación?...Nos vamos todos y tú no puedes venir.
A mí me hubiera gustado seguir allí, pero estaba claro que no era bien recibida, así que salte de la línea, el número dos, que había aparecido pegado a mi, desapareció enseguida y volví al otro lado del muro dejando el signo menos al señor Vicente, que pareció no inmutarse.
Ni siquiera pude hablar una palabra con el número cero, que también desapareció... la verdad es que no hay manera de pillarlo.
Me asomé a ver lo que ocurría en el otro lado y enseguida todo se transformó, la línea, la raíz, mi querido cinco, el espectacular número dos…¡todo desapareció! y en su lugar aparecieron dos números. A uno de ellos pude verle bien, era un precioso tres.
¿Cuál es el otro número que aparece con el tres?¿Puedes ayudar a Fibi y escribir la ecuación de segundo grado donde aparezca con su querido número cinco? ¿Qué número es Matilde?
Etiquetas:
ecuaciones,
matemáticas,
Retos
Suscribirse a:
Comentarios (Atom)